# 3. 树表式查找法
# 1. 二叉排序树
1. 定义:
二叉排序树(Binary Sort Tree)或者是一棵空树;或者是具有下列性质的二叉树:
⑴若左子树不空,则左子树上所有结点的值均小于根结点的值;
⑵若右子树不空,则右子树上所有结点的值均大于根结点的值。
(3) 它的左右子树也都是二叉排序树。
节点存储结构:
typedef struct node{ | |
KeyType key ; /* 关键字的值 */ | |
struct node *lchild,*rchild;/* 左右指针 */ | |
}BSTNode,*BSTree; |
2. 二叉排序树的创建:
举例:记录的关键码序列为:63,90,70,55,67,42,98,83,10,45,58,则构造一棵二叉排序树的过程如下:
即:先读入第一个结点作为根,然后读入第二结点,若第二个结点值大于根,则作根的右子树,否则作左子树…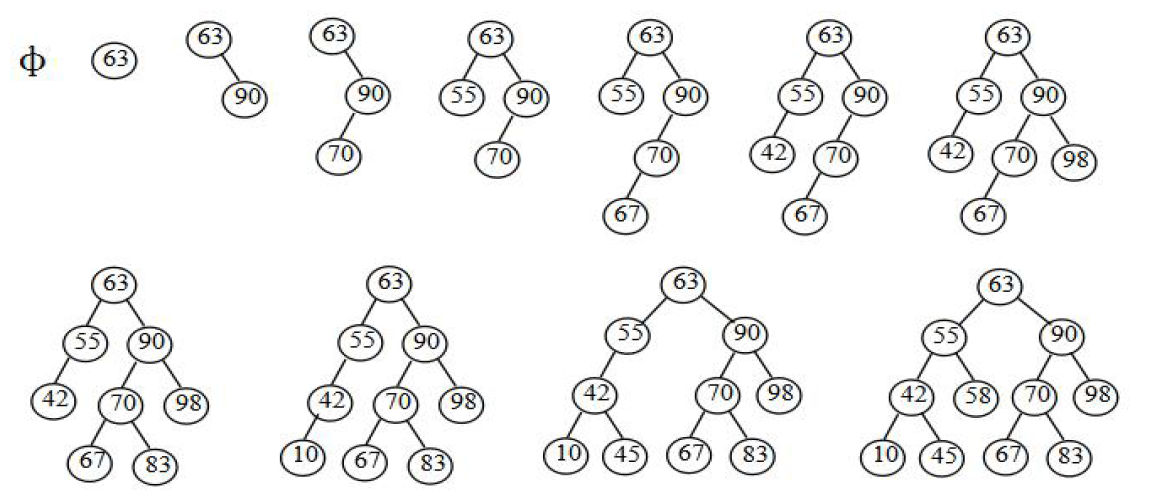
对二叉排序树进行中序遍历,便可得到一个按关键码有序的序列
算法描述:
/* 若在二叉排序树 bst 中不存在关键字等于 key 的元素,插入该元素 */ | |
void InsertBST(BSTree *bst, KeyType key){ | |
BiTree s; | |
if (*bst==NULL){ | |
s=(BSTree)malloc(sizeof(BSTNode));/* 申请新的结点 s*/ | |
s-> key=key; | |
s->lchild=NULL; s->rchild=NULL; | |
*bst=s; | |
} | |
else if (key < (*bst)->key) | |
InsertBST(&((*bst)->lchild), key);/* 将 s 插入左子树 */ | |
else if (key > (*bst)->key) | |
InsertBST(&((*bst)->rchild), key); /* 将 s 插入右子树 */ | |
} | |
// 创建二叉排序树 | |
/* 从键盘输入元素的值,创建相应的二叉排序树 */ | |
void CreateBST(BSTree *bst){ | |
KeyType key; | |
*bst=NULL; | |
scanf("%d",&key); | |
/*EDNKEY 为自定义常量 */ | |
while (key!=ENDKEY){ | |
InsertBST(bst, key); /* 在二叉排序树 bst 中插入结点 key*/ | |
scanf("%d",&key); | |
} | |
} |
3. 二叉排序树的查找:
首先将待查关键字 k 与根结点关键字 t 进行比较,如果:
1) k= t:则返回根结点地址;
2) kt:则进一步查右子树;
3) k>t:则进一步查右子树。
/* 在根指针 bst 所指二叉排序树中,递归查找某关键字等于 key 的元素,若查找成功,返回指向该元素结点指针,否则返回空指针 */ | |
// 二叉排序树查找的递归算法 | |
BSTree SearchBST(BSTree bst, KeyType key){ | |
if (!bst) return NULL; | |
else if (bst->key == key) return bst;/* 查找成功 */ | |
else if (bst->key > key) | |
return SearchBST(bst->lchild, key);/* 在左子树继续查找 */ | |
else | |
return SearchBST(bst->rchild, key);/* 在右子树继续查找 */ | |
} | |
// 二叉排序树查找的非递归算法 | |
BSTree SearchBST(BSTree bst, KeyType key){ | |
BSTree q; | |
q=bst; | |
while(q){ | |
if (q->key == key) return q; /* 查找成功 */ | |
if (q->key > key) q=q->lchild; /* 在左子树中查找 */ | |
else q=q->rchild; /* 在右子树中查找 */ | |
} | |
return NULL; /* 查找失败 */ | |
}/*SearchBST*/ |
4. 二叉排序树的插入:
// 同创建时的插入算法 | |
void InsertBST(BiTree &T, DataType e){ | |
BiTNode *f, *p; | |
p=*T; | |
while(p!=NULL){ | |
if(p->data==e) return; | |
f=p; | |
p=((p->data>e)?p=p->lchild:p=p->rchild) | |
}// 循环完毕 p 为空,f 为插入的父结点 | |
p=(BiTNode*)malloc(sizeof(BiTNode)); | |
P->data=e; | |
p->lchild=NULL; | |
p->rchild=NULL;// 初始化新结点 | |
if(T==NULL) *T=p; | |
else if(p->data>f->data) f->rchild=p; | |
else f->rchild=p; | |
} |
5. 删除:
在查找成功的情况下,删除这个结点,仍满足二叉排序树。
分三种情况:
・删除一个叶子:
只需将被删除结点的父结点相应指针域置空。
・删除的结点只有一棵子树:将子树结点替换父结点。
・删除的结点左右子树均有:
PL 接替 P 成为 F 的子树,PR 成为 PL 最右下结点的右子树
PR 接替 P 成为 F 的子树,PL 成为 PR 最左下结点的左子树
# 2. 二叉平衡树
1. 定义:
又称为 AVL 树,对于一棵非空二叉排序树,它的左子树和右子树都是一棵平衡二叉树,且左子树和右子树的高度之差绝对值不超过 1。
平衡因子:该结点的左子树和右子树高度之差,它的值只能为 - 1、0、1。
2. 构造:
单向左旋、单向右旋、双向旋转(先左后右)、双向旋转(先右后左)
# 3.B - 树
一棵 m 阶的 B - 树,或者是空树,或者是满足下列性质的 m 叉树:
(1) 树中每个结点至多有 m 棵子树;
(2) 根结点至少有两棵子树;
(3) 除根结点之外的非终端结点至少有 m/2 棵子树;
(4) 所有叶子结点都出现在同一层次,可用来 “查找失败” 处理。
首先由根指针 mbt 找到根结点 A,因为 58>37,所以找到结点 C,又因为 40<58<85, 所以找到结点 G,最后在结点 G 中找到 58。如果要查找 32,首先由根指针 mbt 找到根结点 A,因为 32<37,所以找到结点 B,又因为 32>25, 所以找到结点 E,因为 30<32<35, 所以最后找到失败结点 f ,表示 32 不存在,查找失败。
存储结构:
#define m <阶数> | |
typedef int Boolean; | |
typedef struct Mbtnode{ | |
struct Mbtnode *parent ; | |
int keynum ; | |
KeyType key[m+1] ; | |
struct Mbtnode *ptr[m+1]; | |
} Mbtnode, *Mbtree; |
查找:
/* 在根为 mbt 的 B_树中查找关键字 k,如果查找成功,则将所在结点地址放入 np,将结点内位置序号放入 pos,并返回 true;否则,将 k 应被插入的结点地址放入 np,将结点内应插位置序号放入 pos,并返回 false*/ | |
Boolean srch_mbtree (Mbtree mbt, KeyType k, Mbtree *np, int *pos){ | |
p = mbt; | |
fp = NULL; | |
found = false; | |
i = 0; | |
while (p != NULL && !found){ | |
i = search(p, k); | |
if (i>0 && p->key[i] == k) found = true; | |
else { | |
fp = p; | |
p = p->ptr[i]; | |
} | |
} | |
if (found) { | |
*np = p; | |
*pos = i ; | |
return true ; | |
}else { | |
*np = fp; | |
*pos = i; | |
return false ; | |
} | |
} | |
/* 在 mbt 指向的结点中,寻找小于等于 key 的最大关键字序号 */ | |
int search (Mbtree mbt, KeyType key ){ | |
n = mbt->keynum ; | |
i = 1 ; | |
while (i <= n && mbt->key[i] <= key ) i ++; | |
return (i – 1) | |
/* 返回小于等于 key 的最大关键字序号,为 0 时表示应到最左分支找,越界时表示应到最右分支找 */ | |
} |